Παράλληλα σύμπαντα

Η ΥΠΑΡΞΗ ΑΛΛΩΝ ΣΥΜΠΑΝΤΩΝ ΕΙΝΑΙ ΑΜΕΣΗ ΣΥΝΕΠΕΙΑ ΚΟΣΜΟΛΟΓΙΚΩΝ ΠΑΡΑΤΗΡΗΣΕΩΝ
του Μαξ Τέγκμαρκ [1]
Mετάφραση από τα αγγλικά – επιμέλεια: Χρυσούλα Μπουκουβάλα
Υπάρχει άραγε ένα αντίγραφό σας που διαβάζει αυτό το άρθρο; Ένα άτομο που δεν είναι εσείς, αλλά ζει σε έναν πλανήτη που ονομάζεται Γη, με νεφοσκεπή βουνά, εύφορα χωράφια και μεγαπόλεις, σε ένα ηλιακό σύστημα που έχει άλλους οκτώ πλανήτες;
Η ζωή αυτού του προσώπου είναι πανομοιότυπη με τη δική σας από κάθε άποψη. Αλλά εκεί, σ’ αυτόν τον άλλο κόσμο, ίσως αυτός ή αυτή, αποφασίζει τώρα να παρατήσει αυτό το άρθρο χωρίς να το τελειώσει, ενώ εσείς συνεχίζετε να το διαβάζετε.
Η ιδέα ενός τέτοιου άλτερ έγκο ακούγεται περίεργη και αδιανόητη, αλλά απ’ ότι φαίνεται ίσως πρέπει να ζήσουμε μαζί της, καθώς υποστηρίζεται από αστρονομικές παρατηρήσεις. Το απλούστερο και πιο δημοφιλές κοσμολογικό μοντέλο σήμερα, προβλέπει ότι έχετε έναν «διττό», ένα αντίγραφό σας σε έναν γαλαξία περίπου 10 στην 1028 μέτρα από εδώ.
Πρόκειται για μια απόσταση τόσο μεγάλη που ξεφεύγει από το πεδίο των αστρονομικών παρατηρήσεων, αλλά αυτό δεν κάνει τον «διττό» σας λιγότερο πραγματικό. Η εκτίμηση προκύπτει από δεδομένα που θα δούμε παρακάτω και δεν προϋποθέτει καν τις υποθέσεις της σύγχρονης φυσικής, παρά απλώς ότι ο χώρος είναι άπειρος (ή τουλάχιστον αρκετά μεγάλος) σε μέγεθος και σχεδόν ομοιόμορφα γεμάτος με ύλη, όπως δείχνουν οι παρατηρήσεις.
Σε άπειρο χώρο, ακόμη και τα πιο απίθανα γεγονότα πρέπει κάπου να συμβαίνουν. Υπάρχουν απείρως πολλοί άλλοι κατοικημένοι πλανήτες, μεταξύ των οποίων όχι μόνο ένας, αλλά απείρως πολλοί που έχουν ανθρώπους με την ίδια εμφάνιση, όνομα και μνήμες όπως εσείς, οι οποίοι παίζουν κάθε δυνατή παραλλαγή των επιλογών ζωής σας.
Κατά πάσα πιθανότητα δεν θα δείτε ποτέ τους άλλους εαυτούς σας. Η πιο μακρινή απόσταση που μπορείτε να παρατηρήσετε είναι η απόσταση που το φως κατάφερε να ταξιδέψει κατά τα 14 δισεκατομμύρια χρόνια από τότε που άρχισε το Big Bang, η Μεγάλη ‘Εκρηξη.
Τα πιο μακρινά ορατά αντικείμενα είναι τώρα περίπου 4 x 1026 μέτρα μακριά, απόσταση που ορίζει το παρατηρήσιμο [2] σύμπαν μας το οποίο ονομάζεται επίσης Όγκος Χαμπλ (Hubble), Ορίζοντας Παρατήρησης ή απλά «το σύμπαν μας».
Ομοίως, τα σύμπαντα των άλλων εαυτών σας είναι σφαίρες ιδίου μεγέθους με κέντρα τους πλανήτες στους οποίους ζουν αυτοί οι άλλοι εαυτοί. Είναι το πιο απλό παράδειγμα παράλληλων συμπάντων. Κάθε σύμπαν είναι απλώς ένα μικρό κομμάτι ενός μεγαλύτερου Πολυσύμπαντος.
Μ’ αυτό τον ορισμό του «σύμπαντος», θα μπορούσε κανείς να περιμένει ότι η έννοια ενός Πολυσύμπαντος θα μένει για πάντα στον τομέα της μεταφυσικής. Ωστόσο, το όριο μεταξύ φυσικής και μεταφυσικής ορίζεται από το αν μια θεωρία μπορεί να αποδειχτεί πειραματικά, όχι από το αν είναι αλλόκοτη, παράδοξη ή περιλαμβάνει μη παρατηρήσιμες οντότητες.
Τα σύνορα της φυσικής διευρύνθηκαν σταδιακά για να ενσωματώσουν όλο και πιο αφηρημένες (και εν συνεχεία μεταφυσικές) έννοιες όπως η σφαιρική Γη, τα αόρατα ηλεκτρομαγνητικά πεδία, η επιβράδυνση του χρόνου σε υψηλές ταχύτητες, οι κβαντικές υπερθέσεις, ο καμπύλος χώρος και οι μαύρες τρύπες.
Τα τελευταία χρόνια η έννοια του Πολυσύμπαντος έχει προστεθεί σ’ αυτόν τον κατάλογο. Στηρίζεται σε καλά ελεγμένες θεωρίες όπως η σχετικότητα και η κβαντομηχανική και εκπληρώνει και τα δύο βασικά κριτήρια μιας εμπειρικής επιστήμης: κάνει προβλέψεις και μπορεί να τροποποιηθεί.
Οι επιστήμονες έχουν συζητήσει μέχρι τέσσερις διαφορετικούς τύπους παράλληλων συμπάντων. Το θεμελιώδες ερώτημα δεν είναι αν υπάρχει Πολυσύμπαν, αλλά πόσα επίπεδα διαθέτει.
Πολυσύμπαν Επιπέδου Ι: πέρα από τον κοσμολογικό μας ορίζοντα
Τα παράλληλα σύμπαντα με τους εναλλακτικούς εαυτούς σας αποτελούν το Πολυσύμπαν Επιπέδου Ι. Είναι ο λιγότερο αμφιλεγόμενος τύπος Πολυσύμπαντος. Όλοι δεχόμαστε την ύπαρξη πραγμάτων που δεν μπορούμε να δούμε, αλλά θα βλέπαμε αν μετακινούμαστε σ’ ένα πλεονεκτικό σημείο ή απλώς περιμέναμε, όπως οι άνθρωποι που βλέπουν τα πλοία να εμφανίζονται στον ορίζοντα.
Τα αντικείμενα πέρα από τον κοσμολογικό ορίζοντα είναι σε παρόμοια κατάσταση. Το παρατηρούμενο σύμπαν αυξάνεται κατά ένα έτος φωτός κάθε χρόνο, καθώς το φως από πιο μακρυά θέλει χρόνο για να φτάσει σε μας.
Το άπειρο βρίσκεται εκεί, περιμένοντας να το δούμε. Πιθανότατα θα πεθάνετε πολύ πριν γίνουν ορατοί οι άλλοι «διττοί» σας, αλλά βασικά και εάν η κοσμική επέκταση συνεργαστεί, οι απόγονοί σας θα μπορούσαν να τους παρατηρήσουν με ένα αρκετά ισχυρό τηλεσκόπιο.
Αν μη τι άλλο, το Πολυσύμπαν Επιπέδου I ακούγεται προφανές. Είναι ποτέ δυνατόν ο χώρος να μην είναι άπειρος; Υπάρχει καμμιά πινακίδα κάπου που να λέει «Τέλος χώρου εδώ – Προσοχή στο κενό»; Αν ναι, τι βρίσκεται πέρα απ’ αυτόν;
Στην πραγματικότητα, η θεωρία του Αϊνστάιν για τη βαρύτητα αμφισβητεί αυτή την υπόθεση. Ο χώρος είναι πεπερασμένος μόνο εάν έχει κυρτή καμπυλότητα ή ασυνήθιστη τοπολογία.
Ένα σφαιρικό σύμπαν ας πούμε σχήματος κουλουριού, έχει περιορισμένο όγκο και κανένα άκρο. Η μικροκυματική ακτινοβολία υποβάθρου [3] επιτρέπει ευαίσθητες δοκιμές τέτοιων σεναρίων. Μέχρι στιγμής, όμως, τα αποδεικτικά στοιχεία είναι εναντίον τους. Τα μοντέλα ενός άπειρου σύμπαντος ταιριάζουν στα δεδομένα, ενώ τίθενται ισχυροί περιορισμοί στα εναλλακτικά.
Μια άλλη πιθανότητα είναι ο χώρος να είναι άπειρος, αλλά η ύλη να περιορίζεται σε μια πεπερασμένη περιοχή γύρω μας —το ιστορικά δημοφιλές μοντέλο του «σύμπαντος νησίδας».
Σε μια παραλλαγή αυτού του μοντέλου, σε μεγάλες κλίμακες η ύλη αραιώνει υπό μορφήν φράκταλ [4]. Και στις δύο περιπτώσεις, σχεδόν όλα τα σύμπαντα σε ένα Πολυσύμπαν Επιπέδου I θα ήταν άδεια και νεκρά.
Αλλά οι πρόσφατες παρατηρήσεις της τρισδιάστατης κατανομής των γαλαξιών και της μικροκυματικής ακτινοβολίας υποβάθρου, έδειξαν ότι σε μεγάλες κλίμακες η διάταξη της ύλης σε αποστάσεις μεγαλύτερες ακόμα και από 1024 μέτρα δίνει τη θέση της σε συνεκτικές μορφοκλασματικές δομές, χωρίς θαμπή ομοιομορφία του κενού.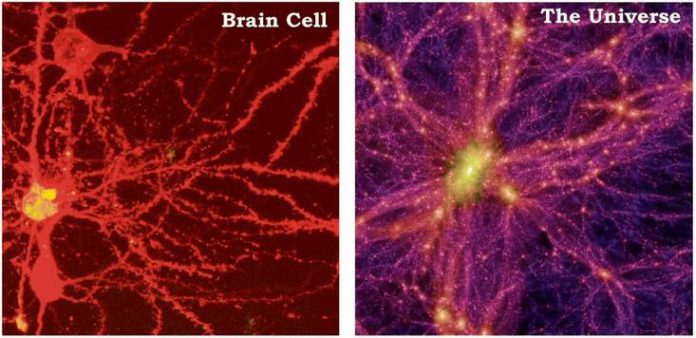

To σύμπαν μας έχει μορφοκλασματική δομή (φράκταλ) παραπέμποντας σε συγκεκριμένο «σκριπτ» και στη θεωρία του ολογράμματος. Γι’ αυτό και ένα εγκεφαλικό κύτταρο (πάνω αριστερά) έχει ίδια μορφή με ένα σμήνος γαλαξιών, η ίριδα (κάτω αριστερά) με ένα νεφέλωμα κλπ.
Οι παρατηρητές που ζουν σε παράλληλα σύμπαντα Επιπέδου Ι βιώνουν τους ίδιους νόμους της φυσικής όπως κι εμείς, αλλά είχαν διαφορετικές αρχικές συνθήκες. Σύμφωνα με τις τρέχουσες θεωρίες, οι διαδικασίες που άρχισαν με τη Μεγάλη Έκρηξη άπλωσαν την ύλη με ένα βαθμό τυχαιότητας, δημιουργώντας όλες τις πιθανές διευθετήσεις (διάφορες του μηδενός).
Οι κοσμολόγοι υποθέτουν ότι οι τιμές που ισχύουν στο σύμπαν μας για τη σχεδόν ομοιόμορφη κατανομή μάζας και για τις αρχικές διακυμάνσεις της πυκνότητας ενός μέρους στα 100.000 είναι πολύ τυπικές (τουλάχιστον για τα σύμπαντα που περιέχουν παρατηρητές).
Αυτή η υπόθεση προκύπτει από την εκτίμηση ότι το πιο κοντινό αντίγραφό σας είναι 10 στην 1028 μέτρα μακριά. Περίπου 10 στην 1092 μέτρα μακριά, θα πρέπει να υπάρχει μια σφαίρα ακτίνας 100 ετών φωτός, πανομοιότυπη με τη δική μας, έτσι όλες οι προσλαμβάνουσες παραστάσεις που θα έχουμε κατά τα επόμενα εκατό χρόνια θα είναι όμοιες με εκείνες των διττών μας εκεί πέρα. Περίπου 10 στην 10118 μέτρα μακριά βρίσκεται ένας ολόκληρος Όγκος Χαμπλ, ίδιος με τον δικό μας (ένα ολόκληρο σύμπαν δηλαδή).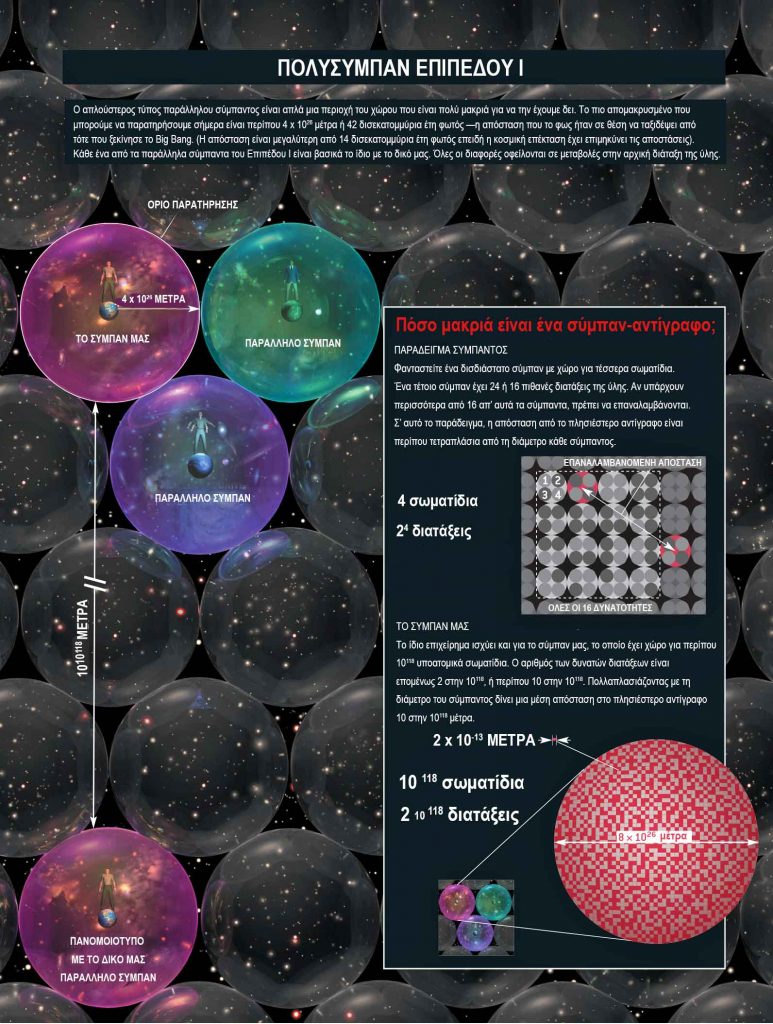
© Scientific American. Προσαρμογή γραφήματος – μετάφραση: «Απεροπία»
Όλες αυτές είναι εξαιρετικά συντηρητικές εκτιμήσεις, που προκύπτουν απλά μετρώντας όλες τις πιθανές κβαντικές καταστάσεις που μπορεί να έχει ένας Όγκος Χαμπλ εάν δεν είναι θερμότερος από 108 βαθμούς Κέλβιν (Κ)[5]. Ένας τρόπος για να κάνετε σχετικούς υπολογισμούς είναι να υπολογίσετε πόσα πρωτόνια μπορούν να χωρέσουν σ’ έναν Όγκο Χαμπλ σε τέτοια θερμοκρασία.
Η απάντηση είναι 10118 πρωτόνια. Καθένα απ’ αυτά τα σωματίδια μπορεί να υπάρχει ή όχι μέσα σ’ έναν τέτοιο όγκο, πράγμα που διπλασιάζει τις 10118 πιθανές διατάξεις τους. Ένα υποθετικό «κουτί» που περιέχει τόσους πολλούς Όγκους Χαμπλ, εξαντλεί λοιπόν όλες τις πιθανότητες.
Αν κάνετε τους υπολογισμούς, ένα τέτοιο κουτί έχει διάμετρο περίπου 10 στην 10118 μέτρα. Πέρα από αυτό το κουτί, τα σύμπαντα — συμπεριλαμβανομένου και του δικού μας— πρέπει να επαναλαμβάνονται. Ο ίδιος αριθμός περίπου θα μπορούσε να προκύψει χρησιμοποιώντας θερμοδυναμικές ή κβαντικές – βαρυτικές εκτιμήσεις του συνολικού πληροφοριακού περιεχομένου του σύμπαντος.
Ο πλησιέστερος διττός σας είναι επομένως πολύ πιθανόν να είναι πολύ κοντύτερά σας απ’ ό,τι υποδεικνύουν αυτοί οι αριθμοί, δεδομένων των διαδικασιών σχηματισμού πλανητών και της βιολογικής εξέλιξης που ανατρέπουν τις πιθανότητες υπέρ σας. Οι αστρονόμοι υποπτεύονται ότι ο δικός μας Όγκος Χαμπλ έχει τουλάχιστον 1020 κατοικήσιμους πλανήτες. Κάποιοι μπορεί να μοιάζουν με τη Γη.
Το πλαίσιο του Πολυσύμπαντος Επιπέδου Ι χρησιμοποιείται συνήθως για την αξιολόγηση θεωριών στη σύγχρονη κοσμολογία, εντούτοις αυτή η διαδικασία σπάνια διατυπώνεται καθαρά. Για παράδειγμα, σκεφτείτε πώς οι κοσμολόγοι χρησιμοποίησαν τα δεδομένα της μικροκυματικής ακτινοβολίας υποβάθρου για να αποκλείσουν μια πεπερασμένη, σφαιρική γεωμετρία του σύμπαντος.
Τα θερμά και ψυχρά σημάδια σε χάρτες μικροκυματικής ακτινοβολίας υποβάθρου έχουν ένα χαρακτηριστικό μέγεθος που εξαρτάται από την καμπυλότητα του χώρου, έτσι τα παρατηρούμενα σημάδια εμφανίζονται πολύ μικρά για να αντιστοιχούν σ’ ένα σύμπαν σφαιρικού σχήματος.
© Scientific American. Προσαρμογή γραφήματος-μετάφραση: «Απεροπία»
Είναι όμως σημαντικό τα συμπεράσματά μας να είναι στατιστικά αυστηρά. Το μέσο μέγεθος του σημαδιού διαφέρει από τον έναν Όγκο Χαμπλ στον άλλον, οπότε είναι πιθανόν ότι το σύμπαν μας μάς ξεγελάει. Μπορεί να είναι σφαιρικό, αλλά να έχει ασυνήθιστα μικρά σημάδια.
Όταν οι κοσμολόγοι λένε ότι έχουν αποκλείσει το σφαιρικό σχήμα του σύμπαντός μας με σιγουριά 99,9%, θέλουν να πουν ότι εάν αυτό το μοντέλο ήταν αληθινό, λιγότεροι από ένας στους χίλιους Όγκους Χαμπλ θα έδειχναν σημάδια τόσο μικρά όσο αυτά που παρατηρούμε στον δικό μας.
Το συμπέρασμα είναι ότι η θεωρία του Πολυσύμπαντος μπορεί να ελεγχθεί και να απορριφθεί ακόμα κι αν δεν μπορούμε να δούμε τα άλλα σύμπαντα. Το κλειδί είναι να προβλέψουμε ποιο μπορεί είναι το σύνολο των παράλληλων συμπάντων και να καθορίσουμε μια κατανομή πιθανοτήτων, ή ποιο είναι αυτό που οι μαθηματικοί αποκαλούν «μέτρο» πάνω σε αυτό το σύνολο.
Το δικό μας σύμπαν τότε πρέπει να προκύψει ως ένα από τα πιο πιθανά. Αν όχι —αν σύμφωνα με τη θεωρία του Πολυσύμπαντος, ζούμε σε ένα ελάχιστα πιθανό σύμπαν— τότε η θεωρία έχει πρόβλημα.
Όπως θα αναλύσω αργότερα, αυτό το πρόβλημα του μέτρου μπορεί να αποδειχτεί αρκετά δύσκολο.
Πολυσύμπαν Επιπέδου II: άλλες φυσαλίδες μετά την πληθωριστική φάση
Αν το Επίπεδο Ι σας έπεσε βαρύ, προσπαθήστε να φανταστείτε ένα άπειρο σύνολο διακριτών Πολυσυμπάντων Επιπέδου Ι, μερικά ίσως με διαφορετικές χωροχρονικές διαστάσεις και φυσικές σταθερές.
Αυτά τα άλλα Πολυσύμπαντα —τα οποία αποτελούν ένα Πολυσύμπαν Επιπέδου ΙΙ— προβλέπονται από την τρέχουσα δημοφιλή θεωρία του χαοτικού αιώνιου πληθωρισμού.
Ο πληθωρισμός είναι μια επέκταση της θεωρίας της Μεγάλης Έκρηξης προσπαθώντας να εξηγήσει πολλά από αδύνατα σημεία της, όπως είναι το γιατί το σύμπαν μας είναι τόσο μεγάλο, τόσο ομοιόμορφο και τόσο επίπεδο.
Μια ταχεία διαστολή του χώρου στις απαρχές του σύμπαντός μας μπορεί να εξηγήσει όλες αυτές, καθώς και άλλες ιδιότητες. Μια τέτοια διαστολή προβλέπεται από μια ευρεία κλίμακα θεωριών των στοιχειωδών σωματιδίων και όλα τα διαθέσιμα στοιχεία τείνουν να υποστηρίξουν μια τέτοιου είδους διαστολή.
Ο ορισμός «χαοτικός αιώνιος» αναφέρεται σ’ αυτό που συμβαίνει σε πολύ μεγαλύτερες κλίμακες. Ο χώρος στο σύνολό του τεντώνεται (διαστέλλεται) και θα συνεχίσει να το κάνει ες αεί, αλλά ορισμένες περιοχές του χώρου σταματούν να τεντώνονται και σχηματίζουν ξεχωριστές φυσαλίδες, όπως σχηματίζονται φουσκάλες αέρα στη ζύμη του ψωμιού που φουσκώνει.
Εμφανίζονται άπειρες τέτοιες φουσκάλες. Η καθεμιά τους αποτελεί ένα εμβρυικό Πολυσύμπαν Επιπέδου I: άπειρο σε μέγεθος και γεμάτο με ύλη που συσσωρεύτηκε εκεί από το ενεργειακό πεδίο που δημιούργησε τον πληθωρισμό.
Αυτές οι φυσαλίδες είναι απείρως μακριά από τη Γη, με την έννοια ότι ποτέ δεν θα φτάσουμε εκεί πέρα, ακόμα κι αν ταξιδεύαμε με την ταχύτητα του φωτός για πάντα. Ο λόγος είναι ότι ο χώρος μεταξύ της φυσαλίδας μας και των γειτονικών της, τεντώνεται πιο γρήγορα από ό, τι θα μπορούσαμε να κινηθούμε μέσα του.
Οι απόγονοί μας δεν θα δουν ποτέ τους διττούς τους μέσα στο Επίπεδο ΙΙ. Για τον ίδιο λόγο, αν η κοσμική διαστολή επιταχυνθεί —όπως δείχνουν οι μέχρι σήμερα παρατηρήσεις— δεν θα δούμε ποτέ τα αντίγραφά μας ακόμη και στο Eπίπεδο Ι.
Το Πολυσύμπαν Επιπέδου ΙΙ είναι πολύ διαφορετικότερο από το Πολυσύμπαν Επιπέδου Ι. Οι φυσαλίδες ποικίλλουν όχι μόνο γιατί έχουν διαφορετικές αρχικές συνθήκες αλλά και στις φαινομενικά αμετάβλητες φυσικές σταθερές τους.
Διάσπαση συμμετριών
Σήμερα η επικρατούσα άποψη στη φυσική είναι ότι οι διαστάσεις του χωροχρόνου, οι ιδιότητες των στοιχειωδών σωματιδίων και πολλές από τις αποκαλούμενες φυσικές σταθερές δεν προκύπτουν από τους φυσικούς νόμους, αλλά είναι το αποτέλεσμα διεργασιών γνωστών ως διασπάσεις συμμετριών.
Για παράδειγμα, οι θεωρητικοί πιστεύουν ότι ο χώρος στο σύμπαν μας είχε κάποτε εννέα διαστάσεις (σημ. μτφρ: σήμερα θεωρείται ότι είχε τουλάχιστον έντεκα), όλες ισότιμες. Στην αρχή της συμπαντικής μας ιστορίας, τρεις απ’ αυτές συμμετείχαν στην διαστολή του και έγιναν οι τρεις διαστάσεις που παρατηρούμε σήμερα (μήκος, πλάτος, ύψος).
Οι υπόλοιπες έξι είναι σήμερα μη παρατηρήσιμες, είτε επειδή έχουν παραμείνει μικροσκοπικές σε μια τοπολογία τόρου ή επειδή όλη η ύλη περιορίζεται σε μια τρισδιάστατη επιφάνεια (μεμβράνη ή απλώς βράνη) που πλέει σε έναν εννεαδιάστατο χώρο.

Σύμπαν με σχήμα τόρου
Έτσι, η αρχική συμμετρία μεταξύ των εννέα διαστάσεων έσπασε. Οι κβαντικές διακυμάνσεις που προκαλούν τον χαοτικό πληθωρισμό θα μπορούσαν να προκαλέσουν διαφορετικά σπασίματα συμμετρίας σε διαφορετικές φυσαλίδες.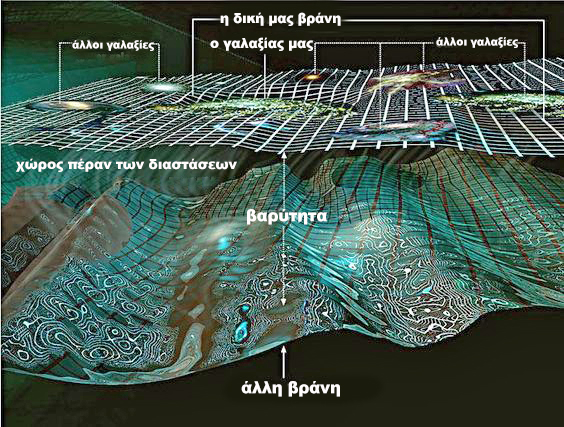

Αναπαράσταση επίπεδων συμπάντων με μορφή βράνης που πλέουν σε πολυδιάστατο χώρο. Προσαρμογή γραφήματος – μετάφραση: “Απεροπία”
Κάποιες μπορεί να έγιναν τετραδιάστατες, άλλες μπορεί να περιέχουν μόνο δύο αντί τρεις γενιές κουάρκ (quarks) [6], ενώ άλλες μπορεί να έχουν μια ισχυρότερη κοσμολογική σταθερά απ’ αυτήν που έχει το σύμπαν μας.
Ένας άλλος τρόπος για την δημιουργία ενός Πολυσύμπαντος Επιπέδου ΙΙ μπορεί να είναι μέσω ενός κύκλου γέννησης και καταστροφής των συμπάντων. Σε επιστημονικό πλαίσιο, αυτή η ιδέα εισήχθη από τον φυσικό Ρίτσαρντ Τόλμαν (Richard Tolman) στη δεκαετία του 1930 και πρόσφατα επεξεργάστηκε από τους Πωλ Στάινχαρντ (Paul Steinhardt) του Πανεπιστημίου Πρίνσετον και Νηλ Τιούροκ (Neil Turok) του Πανεπιστημίου Καίμπριτζ.
Η πρόταση των Στάινχαρντ και Τιούροκ και τα σχετικά μοντέλα περιλαμβάνουν μια δεύτερη, τρισδιάστατη βράνη, που είναι κυριολεκτικά παράλληλη με τη δική μας, απλώς «πλέει» σε μια ανώτερη διάσταση.

© Scientific American. Προσαρμογή γραφήματος – μετάφραση: «Απεροπία»
Αυτό το παράλληλο σύμπαν δεν είναι πραγματικά ένα ξεχωριστό σύμπαν, διότι αλληλεπιδρά με το δικό μας. Αλλά το σύνολο των συμπάντων —παρελθόντων, παρόντων και μελλοντικών— που δημιουργούν αυτές οι βράνες θα αποτελέσει ένα Πολυσύμπαν, αναμφισβήτητα με ποικιλία παρόμοια με εκείνη που παράγεται από τον χαοτικό πληθωρισμό.
Μια ιδέα που προτείνεται από τον φυσικό Λη Σμόλιν (Lee Smolin) του Ινστιτούτου Perimeter του Οντάριο, περιλαμβάνει ένα ακόμη Πολυσύμπαν, συγκρίσιμο σε ποικιλομορφία με αυτό του Επιπέδου ΙΙ, αλλά που διαιρείται συνεχώς σε νέα σύμπαντα που φυτρώνουν μέσω μελανών οπών και όχι μέσω της φυσικής των βρανών.
Παρόλο που δεν μπορούμε να αλληλεπιδράσουμε με άλλα παράλληλα σύμπαντα Επιπέδου ΙΙ, οι κοσμολόγοι μπορούν να συμπεράνουν την παρουσία τους εμμέσως, επειδή η ύπαρξή τους μπορεί να εξηγήσει ανεξήγητες συμπτώσεις στο σύμπαν μας.
Για να καταλάβετε τι θέλω να πω, ας υποθέσουμε ότι πηγαίνετε σ’ ένα ξενοδοχείο και σας δίνουν ένα δωμάτιο με αριθμό 1967 και παρατηρείτε ότι αυτό είναι το έτος που γεννηθήκατε.
«Τι σύμπτωση!» θα πείτε. Μετά από μια στιγμή σκέψης ωστόσο, καταλήγετε στο συμπέρασμα ότι δεν είναι καθόλου περίεργο κάτι τέτοιο. Το ξενοδοχείο διαθέτει εκατοντάδες δωμάτια και το γεγονός δεν θα σας απασχολούσε καθόλου αν σας είχε δοθεί ένα δωμάτιο με αριθμό που δεν σήμαινε τίποτε για σας.
Το συμπέρασμα είναι ότι ακόμη κι αν δεν γνωρίζατε τίποτε από ξενοδοχεία, σίγουρα θα υποθέτατε την ύπαρξη και άλλων δωματίων για να εξηγήσετε μια τέτοια σύμπτωση.
Ας πάρουμε ένα πιο συγκεκριμένο παράδειγμα, τη μάζα του ήλιου μας. Η μάζα ενός άστρου καθορίζει και τη φωτεινότητά του και με βάση τις αρχές της φυσικής υπολογίζουμε ότι η ζωή όπως τη ξέρουμε στη Γη, είναι δυνατή μόνο αν η μάζα ενός ήλιου έχει τιμή μεταξύ 1.6 x 1030 και 2.4 x 1030 κιλά. Διαφορετικά, το κλίμα της Γης θα ήταν ψυχρότερο από αυτό του σημερινού Άρη ή θερμότερο από αυτό της σημερινής Αφροδίτης.
Η μάζα του ήλιου μας είναι 2.0 x 1030 κιλά. Με μια πρώτη ματιά, η ταύτιση της μάζας του ήλιου μας με τις βασικές αρχές της φυσικής και ταυτόχρονα με το ότι η Γη μας είναι κατοικίσιμη, φαίνεται να είναι απόλυτα τυχαία.
Οι μάζες των αστέρων κυμαίνονται από 1029 έως 1032 κιλά, οπότε αν ο ήλιος είχε αποκτήσει τη μάζα που έχει με τυχαίο τρόπο, τότε θα είχε μόνο λίγες πιθανότητες η τιμή της μάζας του να διευκόλυνε την ύπαρξη μιας κατοικίσιμης Γης.
Αλλά όπως ακριβώς και στο παράδειγμα του ξενοδοχείου, μπορεί κανείς να εξηγήσει αυτή την προφανή σύμπτωση, αποδεχόμενος ένα σύνολο (στην περίπτωση αυτή έναν αριθμό από πλανητικά συστήματα) και ένα νόμο επιλογής (το γεγονός ότι πρέπει να ζούμε σ’ έναν κατοικήσιμο πλανήτη).
Τέτοιες επιλογές που σχετίζονται με παρατηρητές αναφέρονται ως «ανθρωπικές». Οι φυσικοί δε συμφωνούν ευρέως ότι πρέπει να μη ληφθούν υπ΄όψιν κατά τον έλεγχο θεμελιωδών θεωριών.
Ό,τι ισχύει για τα δωμάτια ξενοδοχείου και για τα πλανητικά συστήματα ισχύει και για τα παράλληλα σύμπαντα. Τα περισσότερα, αν όχι όλα από τα χαρακτηριστικά που καθορίζονται από το σπάσιμο της συμμετρίας, φαίνεται να είναι καλά συντονισμένα.
Αλλάζοντας πανελάχιστα τις τιμές τους θα είχαμε ένα ποιοτικά διαφορετικό σύμπαν —ένα σύμπαν στο οποίο πιθανότατα δεν θα υπήρχαμε. Αν τα πρωτόνια ήταν 0,2 % βαρύτερα, θα διασπώνταν σε νετρόνια, αποσταθεροποιώντας τα άτομα.
Αν η ηλεκτρομαγνητική δύναμη ήταν 4% ασθενέστερη, δεν θα υπήρχε υδρογόνο και συνήθη αστέρια. Αν η ασθενής αλληλεπίδραση ήταν πολύ ασθενέστερη, το υδρογόνο δεν θα υπήρχε. Αν ήταν πολύ ισχυρότερη, οι σουπερνόβα θα αποτύγχαναν να διασπείρουν βαριά στοιχεία στον διαστρικό χώρο. Αν η κοσμολογική σταθερά ήταν πολύ μεγαλύτερη, το σύμπαν θα είχε διασταλεί τόσο πολύ, ώστε θα είχε σκάσει πριν σχηματιστούν οι πρώτοι γαλαξίες.
Παρόλο που ο βαθμός αυτής της αρμονίας είναι ακόμα συζητήσιμος, τα παραδείγματα αυτά υποδηλώνουν την ύπαρξη παράλληλων συμπάντων που έχουν διαφορετικές τιμές φυσικών σταθερών.
Η θεωρία των Πολυσυμπάντων Επιπέδου ΙΙ προβλέπει ότι οι φυσικοί δεν θα είναι ποτέ σε θέση να καθορίσουν τις τιμές αυτών των σταθερών στηριζόμενοι στις δικές μας βασικές αρχές.
Θα υπολογίσουν απλώς τις κατανομές πιθανοτήτων για το τι περιμένουν να βρουν, με βάση τους νόμους επιλογής. Το αποτέλεσμα θα πρέπει να είναι τόσο γενικό, όσο να επιτρέπει βεβαίως και την ύπαρξή μας.
Πολυσύμπαν Επιπέδου ΙΙΙ: πολλαπλοί κβαντικοί κόσμοι
Τα Πολυσύμπαντα Επιπέδου I και II περιλαμβάνουν παράλληλους κόσμους που είναι πολύ μακριά, ακόμα πιο πέρα από τον τομέα μελέτης των αστρονόμων. Το επόμενο όμως επίπεδο Πολυσύμπαντος βρίσκεται ακριβώς γύρω σας. Πώς γίνεται αυτό;
Προκύπτει από τη διάσημη, περίφημη και αμφιλεγόμενη ερμηνεία της κβαντομηχανικής των πολλών κόσμων, δηλαδή από την ιδέα ότι οι τυχαίες κβαντικές διαδικασίες αναγκάζουν το σύμπαν να διακλαδιστεί σε πολλαπλά αντίγραφα, ένα για κάθε πιθανό αποτέλεσμα που λαμβάνεται σε κβαντικό επίπεδο.
Στις αρχές του 20ού αιώνα η θεωρία της κβαντομηχανικής προκάλεσε επανάσταση στη φυσική, εξηγώντας το ατομικό πεδίο, με τη διαφορά ότι αυτή η ερμηνεία δεν συμφωνούσε με τους κανόνες της Νευτώνειας μηχανικής.
Κυματοσυνάρτηση και αιτιοκρατία
Παρά τις προφανείς επιτυχίες της θεωρίας, υπήρχε έντονη διαμάχη για το τι πραγματικά σήμαινε. Η θεωρία καθορίζει την κατάσταση του σύμπαντος όχι με κλασσικούς όρους, όπως οι θέσεις και οι ταχύτητες όλων των σωματιδίων, αλλά από την άποψη ενός μαθηματικού αντικειμένου που ονομάζεται κυματοσυνάρτηση [7].
Σύμφωνα με την εξίσωση του Έρβιν Σρέτινγκερ (Erwin Schrödinger) [8], αυτή η κατάσταση εξελίσσεται με την πάροδο του χρόνου κατά έναν τρόπο που οι μαθηματικοί ονομάζουν «μοναδιαίο», που σημαίνει ότι η κυματοσυνάρτηση περιστρέφεται σε έναν αφηρημένο χώρο άπειρων διαστάσεων που ονομάζεται χώρος Χίλμπερτ [9].
Αν και η κβαντομηχανική περιγράφεται συχνά ως εγγενώς τυχαία και αβέβαιη, εντούτοις η κυματοσυνάρτηση εξελίσσεται με έναν αιτιοκρατικό τρόπο. Δεν υπάρχει τίποτα τυχαίο ή αβέβαιο σ’ αυτήν την εξέλιξη.
Η ουσία είναι πώς να συνδέσουμε τη κυματοσυνάρτηση μ’ αυτό που παρατηρούμε. Πολλές αποδεκτές κυματοσυναρτήσεις αντιστοιχούν σε καταστάσεις μη κατανοητές από τη λογική μας, όπως το παράδειγμα του νοητικού πειράματος της Γάτας του Σρέτινγκερ [10] που για τον παρατηρητή είναι ταυτόχρονα νεκρή και ζωντανή σε μια κατάσταση επονομαζόμενη υπέρθεση κατά την οποία οι δύο πιθανές καταστάσεις (νεκρή/ζωντανή) αναμειγνύονται σε επαλληλία.

Αναπαράσταση επαλληλίας καταστάσεων γάτας του Σρέτινγκερ
Στη δεκαετία του 1920 οι φυσικοί εξήγησαν αυτή την παράξενη κατάσταση, υποθέτοντας ότι η κυματοσυνάρτηση «κατέρρεε» σε κάποιο συγκεκριμένο αποτέλεσμα, όποτε δηλαδή κάποιος παρατηρούσε το σύστημα.
Η επινόηση της κατάρρευσης της κυματοσυνάρτησης είχε μεν την αρετή να εξηγεί τις παρατηρήσεις, αλλά έκανε μια κομψή και ενιαία θεωρία, σκοτεινή και μη ενιαία. Η εγγενής τυχαιότητα που συνήθως αποδίδεται στην κβαντομηχανική είναι το αποτέλεσμα αυτής της υπόθεσης.
Με την πάροδο των ετών, πολλοί φυσικοί έχουν εγκαταλείψει αυτήν την άποψη υπέρ μιας που αναπτύχθηκε το 1957 από τον μεταπτυχιακό φοιτητή του Πρίνσετον, Χιου Έβερετ (Hugh Everett). Ο Έβερετ έδειξε ότι η κατάρρευση της κυματοσυνάρτησης δεν είναι απαραίτητη. Η κβαντική θεωρία αυτή καθεαυτή, στην πραγματικότητα, δεν δημιουργεί αντιφάσεις.
Υπερθέσεις πολλών κόσμων
Αν και η θεωρία προβλέπει ότι μια κλασική πραγματικότητα χωρίζεται σε υπερθέσεις πολλών τέτοιων πραγματικοτήτων, οι παρατηρητές υποκειμενικά αντιλαμβάνονται αυτόν τον διαχωρισμό ως μια ελαφρά τυχαιότητα, με πιθανότητες σε πλήρη συμφωνία μ’ αυτές που προβλέπονταν από το παλιό αξίωμα της κατάρρευσης. Αυτή η υπέρθεση των κλασσικών κόσμων αποτελεί τοΠολυσύμπαν Επιπέδου ΙΙΙ.
© Scientific American. Προσαρμογή γραφήματος-μετάφραση: «Απεροπία»
Η ερμηνεία των πολλών κόσμων του Έβερετ ταρακούνησε τα νερά μέσα και έξω από τη κοινότητα των φυσικών για περισσότερο από τέσσερις δεκαετίες. Μια θεωρία γίνεται πιο εύκολη στην κατανόησή της, όταν ένας φυσικός διακρίνει δύο τρόπους αντιμετώπισης μιας φυσικής θεωρίας: την προοπτική που έχει ένας φυσικός που μελετά τις μαθηματικές της εξισώσεις ΑΠΟ ΨΗΛΑ, σαν ένα πουλί που ίπταται ερευνώντας ένα τοπίο από ψηλά, και την προοπτική ενός παρατηρητή που ζει XAMHΛΑ, δηλαδή ΜΕΣΑ στον κόσμο που περιγράφεται από τις εξισώσεις, σαν ένας βάτραχος που ζει μέσα στο τοπίο που βλέπει το πουλί που υπερίπταται.
Από την προοπτική του πουλιού, το Πολυσύμπαν Επιπέδου ΙΙΙ είναι απλό. Υπάρχει μόνο μία κυματοσυνάρτηση. Εξελίσσεται ομαλά και προκαθοριστικά με την πάροδο του χρόνου, χωρίς κανένα είδος διαχωρισμού ή παραλληλίας.
Ο αφηρημένος κβαντικός κόσμος που περιγράφεται από αυτήν την εξελισσόμενη κυματοσυνάρτηση περιέχει μέσα του ένα τεράστιο αριθμό παράλληλων κλασικών εκδοχών ιστορίας, συνεχούς διαχωρισμού και συγχώνευσης, καθώς και μια σειρά κβαντικών φαινομένων που στερούνται κλασσικής περιγραφής.
Από την προοπτική τους σαν βάτραχοι, οι παρατηρητές αντιλαμβάνονται μόνο ένα μικρό κλάσμα αυτής της πλήρους πραγματικότητας. Μπορούν να δουν το δικό τους σύμπαν Επιπέδου Ι, αλλά μια διαδικασία που ονομάζεται αποσυνοχή (decoherence) —η οποία μιμείται την κατάρρευση της κυματοσυνάρτησης διατηρώντας ταυτόχρονα τη μοναδικότητα—τους εμποδίζει να δουν τα Επιπέδου ΙΙΙ παράλληλα αντίγραφα του εαυτού τους.

Το σύμπαν μας πιθανόν να έχει σχήμα τόρου
Κάθε φορά που ζητείται από τους παρατηρητές να πάρουν μια γρήγορη απόφαση και να δώσουν μια απάντηση, οι κβαντικές επιδράσεις στους εγκεφάλους τους τους οδηγούν σε μια υπέρθεση των αποτελεσμάτων, όπως «Συνέχισε να διαβάζεις αυτό το άρθρο» και «Σταμάτα να διαβάζεις αυτό το άρθρο».
Για την αντιληπτικότητα του πουλιού η πράξη λήψης απόφασης προκαλεί τη διάσπαση ενός ατόμου σε πολλαπλά αντίγραφα: ένα που συνεχίζει να διαβάζει και ένα που σταματά.
Για την αντιληπτικότητα του βατράχου όμως, καθένα από αυτά τα άλτερ έγκο δεν γνωρίζει ότι υπάρχουν τα άλλα και θεωρεί τη πιθανότητα εναλλακτικού μέλλοντος απλώς ως μια ελαφρά τυχαιότητα, θεωρεί δηλαδή πως υπάρχει μια κάποια πιθανότητα να συνεχίσει να διαβάζει ένα άρθρο και μια άλλη να μη συνεχίσει.
Όσο περίεργο μπορεί να ακούγεται αυτό, η ίδια ακριβώς κατάσταση παρατηρείται ακόμη και στο Πολυσύμπαν Επιπέδου Ι. Έχετε προφανώς αποφασίσει να συνεχίσετε να διαβάζετε το άρθρο, αλλά ένας από τους «σωσίες» σας σε ένα μακρινό γαλαξία παράτησε το διάβασμα του περιοδικού μετά την πρώτη παράγραφο.
Η μόνη διαφορά μεταξύ του Επιπέδου Ι και του Επιπέδου ΙΙΙ είναι πού κατοικεί ο σωσίας σας. Στο Επίπεδο Ι ζει αλλού, στον παλιό καλό τρισδιάστατο χώρο. Στο Επίπεδο ΙΙΙ ζει σε ένα άλλο κβαντικό παρακλάδι του απειροδιάστατου χώρου Χίλμπερτ.
Η ύπαρξη του Επιπέδου ΙΙΙ εξαρτάται από μία κρίσιμη υπόθεση: ότι η χρονική εξέλιξη της κυματοσυνάρτησης είναι μοναδιαία. Μέχρι στιγμής τα πειραματικά δεδομένα δεν είχαν αποκλίσεις από την μοναδιαία ιδιότητα.
Τις τελευταίες δεκαετίες οι επιστήμονες επιβεβαίωσαν την μοναδιαία ιδιότητα σε ολοένα και μεγαλύτερα συστήματα, συμπεριλαμβανομένων των μπανκμιστερφουλερένιων (είδος ανθρακικών δομών εξήντα μορίων) και των οπτικών ινών μήκους χιλιομέτρων.
Από θεωρητικής πλευράς, η περίπτωση της μοναδιαίας ιδιότητας έχει ενισχυθεί από την ανακάλυψη της αποσυνοχής. Μερικοί θεωρητικοί που εργάζονται πάνω στην κβαντική βαρύτητα αμφισβήτησαν τη μοναδιαία ιδιότητα. Μια σχετική περίπτωση είναι ότι η εξάτμιση των μελανών οπών μπορεί να καταστρέψει τις πληροφορίες, κάτι που θα ήταν μια μη μοναδιαία διαδικασία.
Αλλά μια πρόσφατη ανακάλυψη στη θεωρία των χορδών γνωστή ως «Αντιστοιχία AdS / CFT» υποδηλώνει ότι ακόμη και η κβαντική βαρύτητα είναι μοναδιαία. Επομένως, οι μελανές οπές δεν καταστρέφουν τις πληροφορίες αλλά απλώς τις διοχετεύουν αλλού.
Εάν στη φυσική ισχύει η μοναδιαία ιδιότητα, τότε πρέπει να αλλάξει η τυπική εικόνα του τρόπου με τον οποίο λειτουργούσαν οι κβαντικές διακυμάνσεις στην αρχή της Μεγάλης Έκρηξης. Αυτές οι διακυμάνσεις δεν παρήγαγαν τις αρχικές συνθήκες στην τύχη.
Αντιθέτως, δημιουργούσαν μια κβαντική υπέρθεση όλων των πιθανών αρχικών συνθηκών, οι οποίες συνυπήρχαν ταυτόχρονα. Στη συνέχεια, η αποσυνοχή εξανάγκασε αυτές τις αρχικές συνθήκες να συμπεριφέρονται κλασικά και να ακολουθήσουν ξεχωριστούς κβαντικούς κλάδους.
Εργοδικότητα
Κι εδώ βρίσκεται το κρίσιμο σημείο: η κατανομή των πιθανών αποτελεσμάτων σε διαφορετικούς κβαντικούς κλάδους σε ένα δεδομένο Όγκο Χαμπλ (Επίπεδο ΙΙΙ) είναι ταυτόσημη με τη κατανομή των αποτελεσμάτων σε διαφορετικούς Όγκους Χαμπλ μέσα σε ένα μοναδικό κβαντικό κλάδο (Επίπεδο Ι). Αυτή η ιδιότητα των κβαντικών διακυμάνσεων είναι γνωστή στη στατιστική μηχανική ως εργοδικότητα.
Ο ίδιος συλλογισμός ισχύει και για το Επίπεδο ΙΙ. Η διαδικασία της διάσπασης της συμμετρίας δεν παράγει ένα μοναδικό αποτέλεσμα, αλλά μάλλον μια υπέρθεση όλων των αποτελεσμάτων, τα οποία γρήγορα ακολουθούν το καθένα ξεχωριστό δρόμο.
Έτσι, αν οι φυσικές σταθερές, οι διαστάσεις του χώρου και ούτω καθεξής μπορούν να διαφέρουν μεταξύ των παράλληλων κβαντικών κλάδων Επιπέδου ΙΙΙ, τότε θα διαφέρουν και μεταξύ των παράλληλων συμπάντων Επιπέδου ΙΙ.
Μ’ άλλα λόγια, το Πολυσύμπαν Επιπέδου ΙΙΙ δεν προσθέτει τίποτα νέο πέραν του Επιπέδου Ι και του Επιπέδου ΙΙ, απλώς πιο διακριτά αντίγραφα των ίδιων συμπάντων —ίδιες παλιές γραμμές ιστορίας που παίζουν ξανά και ξανά σε άλλους κβαντικούς κλάδους.
Η παθιασμένη συζήτηση σχετικά με τη θεωρία του Έβερετ φαίνεται να τελειώνει άδοξα με την ανακάλυψη λιγότερο αμφισβητούμενων Πολυσυμπάντων (Επίπεδα I και II) που είναι εξίσου τεράστια.
Περιττό να πούμε ότι οι συνέπειες είναι βαθιές και οι φυσικοί αρχίζουν να τις εξερευνούν. Για παράδειγμα, εξετάστε τις συνέπειες της απάντησης σε μια παλιά ερώτηση: αυξάνεται εκθετικά ο αριθμός των συμπάντων με την πάροδο του χρόνου;
Η εκπληκτική απάντηση είναι όχι. Κατά την αντιληπτικότητα του πουλιού, φυσικά υπάρχει μόνο ένα κβαντικό σύμπαν. Κατά την αντιληπτικότητα του βατράχου αυτό που έχει σημασία είναι ο αριθμός των συμπάντων που είναι διακριτά μεταξύ τους σε μια δεδομένη στιγμή —δηλαδή ο αριθμός των αξιοσημείωτα διαφορετικών Όγκων Χαμπλ.
Φανταστείτε ότι οι πλανήτες μετακινούνται σε νέες τυχαίες θέσεις, ότι έχετε παντρευτεί κάποιαν άλλη και ούτω καθεξής. Σε κβαντικό επίπεδο, υπάρχουν 10 στην 10118 σύμπαντα με θερμοκρασίες κάτω από 108 Κέλβιν. Αυτός είναι μεν ένας τεράστιος αριθμός, αλλά πεπερασμένος.
Από την προοπτική του βατράχου, η εξέλιξη της κυματοσυνάρτησης αντιστοιχεί σε μια ατέρμονα ολίσθηση από μιά από αυτές τις 10 στην 10118 καταστάσεις σε μια άλλη.
Τώρα είστε στο σύμπαν Α, εκείνο στο οποίο διαβάζετε αυτήν την πρόταση. Έπειτα βρίσκεστε στο σύμπαν Β, εκείνο στο οποίο διαβάζετε αυτήν την άλλη πρόταση. Μ’ άλλα λόγια, το σύμπαν Β έχει έναν παρατηρητή ταυτόσημο μ’ αυτόν του σύμπαντος Α, εκτός από το ότι αυτός έχει μια επιπλέον μνήμη μιας πρόσθετης στιγμής.
Όλες οι πιθανές καταστάσεις υπάρχουν σε κάθε στιγμή, οπότε η αίσθηση του περάσματος του χρόνου μπορεί κάλλιστα να οφείλεται στο αισθητήριο οπτικό όργανο του παρατηρητή, δηλαδή στο μάτι, μια ιδέα που διερευνήθηκε το 1994 στο μυθιστόρημα επιστημονικής φαντασίας με τίτλο Permutation City (Η πόλη της μετάθεσης) του Γκρεγκ Έγκαν (Greg Egan), και αναπτύχθηκε από τους φυσικούς Ντέιβιντ Ντόιτς (David Deutsch) της Οξφόρδης, Τζούλιαν Μπάρμπουρ (Julian Barbour) και άλλους.
Επομένως, η λύση για την κατανόηση της φύσης του χρόνου μπορεί να βρίσκεται στην ύπαρξη Πολυσυμπάντων.
Πολυσύμπαν Επιπέδου IV: άλλες μαθηματικές κατασκευές
Οι αρχικές συνθήκες και οι φυσικές σταθερές στα Πολυσύμπαντα Επιπέδου Ι, ΙΙ και ΙΙΙ μπορεί να ποικίλουν, αλλά οι θεμελιώδεις νόμοι που διέπουν τη φύση παραμένουν οι ίδιοι.
Υπάρχει σύμπαν που υπακούει στους νόμους της κλασικής φυσικής, αλλά χωρίς να υφίσταται τις κβαντικές συνέπειες; Προχωράει ο χρόνος με διακριτά βήματα, όπως στους υπολογιστές, αντί να είναι συνεχής; Υπάρχει σύμπαν που είναι απλά ένα άδειο δωδεκάεδρο; Στο Πολυσύμπαν Επιπέδου IV, όλες αυτές οι εναλλακτικές πραγματικότητες όντως υπάρχουν.

Προσομοίωση μυστηριώδους μαθηματικής δομής που μπορεί να υπάρχει στην πραγματικότητα με μορφή σύμπαντος
Μια ένδειξη ότι ένα τέτοιο πολυσύμπαν μπορεί να μην είναι μόνο υποθετικό, είναι η στενή αντιστοιχία μεταξύ των κόσμων της αφηρημένης σκέψης και της παρατηρούμενης πραγματικότητας.
Οι εξισώσεις και, γενικότερα, οι μαθηματικές δομές όπως οι αριθμοί, τα γραμμικά και τα γεωμετρικά αντικείμενα περιγράφουν τον κόσμο με αξιοσημείωτη αληθοφάνεια.
Σε μια περίφημη διάλεξη του 1959, ο φυσικός Γιουτζήν Ουίγκνερ (Eugene P. Wigner) υποστήριξε ότι «η τεράστια χρησιμότητα των μαθηματικών στις φυσικές επιστήμες είναι κάτι που συνορεύει με το μυστηριώδες».
Αντιστρόφως, οι μαθηματικές δομές δίνουν μια παράξενη αίσθηση. Πληρούν ένα κεντρικό κριτήριο αντικειμενικής ύπαρξης: είναι ίδιες ανεξάρτητα από το ποιος τις μελετά.Ένα θεώρημα είναι αληθές, ανεξάρτητα από το αν αποδεικνύεται από έναν άνθρωπο, έναν υπολογιστή ή ένα ευφυές δελφίνι.
Οι προηγμένοι εξωγήινοι πολιτισμοί θα ανακάλυπταν τις ίδιες μαθηματικές δομές μ’ αυτές που ανακαλύψαμε κι εμείς. Γι’ αυτό οι μαθηματικοί λένε συνήθως ότι ανακαλύπτουν τις μαθηματικές δομές, δεν τις δημιουργούν.
Αριστοτέλεια ή πλατωνική κοσμοθεώρηση;
Υπάρχουν δύο αξιόλογα αλλά διαμετρικά αντίθετα παραδείγματα για την κατανόηση της αντιστοιχίας μεταξύ των μαθηματικών και της φυσικής, μια διχογνωμία που ξεκινάει από πολύ παλιά, από την εποχή του Πλάτωνα και του Αριστοτέλη.
Σύμφωνα με την αριστοτέλεια κοσμοθεώρηση, η φυσική πραγματικότητα είναι θεμελιώδης και η μαθηματική γλώσσα είναι απλά μια χρήσιμη προσέγγισή της. Σύμφωνα με την πλατωνική κοσμοθεώρηση, η μαθηματική δομή είναι η αληθινή πραγματικότητα, την οποία όμως εμείς ως παρατηρητές αντιλαμβανόμαστε ατελώς.

Kι άλλη περίεργη μαθηματική δομή σε προσομοίωση φυσικής υπόστασης
Μ’ άλλα λόγια, οι δύο κοσμοθεωρήσεις διαφωνούν ως προς το ποια είναι η πιο βασική αντίληψη για τους φυσικούς νόμους: εκείνη του βατράχου-παρατηρητή ή εκείνη του πουλιού-παρατηρητή; Η αριστοτέλεια κοσμοθεώρηση υιοθετεί την αντίληψη του βατράχου, ενώ η πλατωνική του πουλιού.
Όταν είμαστε παιδιά, πολύ πριν ακούσουμε το παραμικρό για μαθηματικά, όλοι μας λειτουργούσαμε σύμφωνα με το αριστοτέλειο πρότυπο. Πολύ αργότερα σχηματίσαμε πλατωνική άποψη για τον κόσμο μας.
Οι σύγχρονοι θεωρητικοί φυσικοί όμως τείνουν να είναι πλατωνιστές, υποψιαζόμενοι ότι τα μαθηματικά περιγράφουν το σύμπαν τόσο καλά, επειδή το σύμπαν είναι εγγενώς μαθηματικό.

© Scientific American. Προσαρμογή γραφήματος – μετάφραση: «Απεροπία»
Κατά συνέπειαν, όλη η φυσική καθίσταται τελικά ένα μαθηματικό πρόβλημα: ένας μαθηματικός με απεριόριστη νοημοσύνη και εργαλεία θα μπορούσε καταρχήν να υπολογίσει την κοσμοθέαση του βατράχου, δηλαδή τι αντιλαμβάνονται παρατηρητές με αυτοσυνείδηση ότι περιέχει το σύμπαν, με ποιους τρόπους το αντιλαμβάνονται και ποιες γλώσσες επινοούν για να περιγράφουν μεταξύ τους τι ακριβώς αντιλαμβάνονται.
Μια μαθηματική δομή είναι μια αφηρημένη, αμετάβλητη οντότητα που υπάρχει έξω από το χώρο και το χρόνο. Αν η ιστορία ήταν μια κινηματογραφική ταινία, η δομή θα αντιστοιχούσε όχι σε μια μόνο σκηνή, αλλά σε ολόκληρη τη ταινία.
Εξετάστε, για παράδειγμα, έναν κόσμο που αποτελείται από σημειακά σωματίδια που κινούνται μέσα σ’ έναν τρισδιάστατο χώρο.
Στον τετραδιάστατο χωρόχρονο —που αντιστοιχεί δηλαδή στην προοπτική του πουλιού— οι τροχιές αυτών των σωματιδίων μοιάζουν με μπερδεμένα μακαρόνια.
Αν ο βάτραχος βλέπει ένα σωματίδιο που κινείται με σταθερή ταχύτητα, το πουλί βλέπει ένα ίσιο, (ας πούμε) ωμό μακαρόνι. Αν ο βάτραχος βλέπει ένα ζευγάρι περιστρεφόμενων σωματιδίων, το πουλί βλέπει δύο (ας πούμε) βρασμένα μακαρόνια μπερδεμένα μεταξύ τους σαν σε διπλή έλικα.
Για τον βάτραχο, ο κόσμος περιγράφεται από τους νευτώνιους νόμους της κίνησης και της βαρύτητας. Για το πουλί, περιγράφεται από τη γεωμετρία των ζυμαρικών, από μια μαθηματική δομή. Ο ίδιος ο βάτραχος είναι απλά μια παχιά δέσμη μακαρονιών, της οποίας η εξαιρετικά πολύπλοκη αλληλεπίδραση αντιστοιχεί σε ένα σύνολο σωματιδίων που αποθηκεύουν και επεξεργάζονται πληροφορίες.
Το σύμπαν μας είναι βέβαια πολύ πιο περίπλοκο απ’ αυτό το παράδειγμα και οι επιστήμονες δεν γνωρίζουν ακόμα σε ποια μαθηματική δομή αντιστοιχεί (αν υπάρχει καμμιά τέτοια). Η πλατωνική κοσμοθεώρηση εγείρει το ερώτημα «γιατί το σύμπαν μας είναι φτιαγμένο μ’ αυτόν τον τρόπο;»
Για έναν αριστοτελικό, αυτό είναι ένα άσκοπο ερώτημα: το σύμπαν απλώς υπάρχει. Αλλά ένας πλατωνικός δεν μπορεί παρά να αναρωτηθεί γιατί δεν θα μπορούσε να υπάρξει αλλιώς.
Αν το σύμπαν μας είναι εγγενώς μαθηματικό, τότε γιατί επιλέχθηκε μόνο μία από τις πολλές δυνατές μαθηματικές δομές για να το περιγράψει; Φαίνεται να υπάρχει μια θεμελιώδης ασυμμετρία στην ίδια την καρδιά της πραγματικότητας.
Σαν διέξοδο απ’ αυτό το τραγικό ερώτημα πρότεινα ότι στον κόσμο μας υπάρχει πλήρης μαθηματική συμμετρία: όλες δηλαδή οι μαθηματικές δομές υπάρχουν επίσης και σε φυσική κατάσταση. Κάθε μαθηματική δομή λοιπόν αντιστοιχεί σ’ ένα παράλληλο σύμπαν.
Τα στοιχεία αυτού του Πολυσύμπαντος δεν υπάρχουν στον ίδιο χώρο, αλλά εκτός χώρου και χρόνου. Τα πιο πολλά απ’ αυτά τα σύμπαντα είναι πιθανώς χωρίς παρατηρητές.
Αυτή η υπόθεση μπορεί να θεωρηθεί ως μια μορφή ριζοσπαστικού πλατωνισμού, υποστηρίζοντας ότι οι μαθηματικές δομές στον πλατωνικό χώρο των ιδεών ή το «διανοητικό τοπίο» [11] του μαθηματικού Ρούντι Ράκερ (Rudy Rucker), έχει φυσική υπόσταση.

Πίνακας του Ρούντι Ράκερ εμπνευσμένος από τα παράλληλα σύμπαντα
Είναι κάτι παρόμοιο μ’ αυτό που ο κοσμολόγος Τζον Μπάροου (John D. Barrow) του Πανεπιστημίου του Καίμπριτζ αποκαλεί «Ουράνιο π» [12], μ’ αυτό που ο φιλόσοφος Ρόμπερτ Νόζικ (Robert Nozick) του Πανεπιστημίου Χάρβαρντ ονόμασε «αρχή της γονιμότητας» ή μ’ αυτό που ονομάστηκε από τον αείμνηστο φιλόσοφο του Πρίνστον Ντέιβιντ Λιούις (David K. Lewis) «μορφολογικός ρεαλισμός».
Η υπόθεση του Πολυσύμπαντος Επιπέδου IV κλείνει την ιεραρχία των πολυσυμπάντων, επειδή οποιαδήποτε αυθύπαρκτη θεμελιώδης φυσική θεωρία μπορεί να διατυπωθεί ως κάποιο είδος μαθηματικής δομής.
Καθώς οι μαθηματικοί συνεχίζουν να κατηγοριοποιούν τις μαθηματικές δομές, θα πρέπει να διαπιστώσουν ότι η δομή που περιγράφει τον κόσμο μας είναι η πιο γενική που είναι ταυτόχρονα και συνεπής και με τις παρατηρήσεις μας.
Αντιστοίχως, οι μελλοντικές μας παρατηρήσεις θα πρέπει να είναι οι πιο γενικές που ταυτόχρονα είναι συνεπείς με τις προηγούμενες παρατηρήσεις μας και οι προηγούμενες παρατηρήσεις μας πρέπει να είναι οι πιο γενικές που είναι συνεπείς με την ύπαρξή μας.
Προσδιορίζοντας την έννοια «γενική» διαπιστώνουμε ότι υπάρχει σοβαρό πρόβλημα, ενώ μάλιστα μόλις τώρα αρχίζει αυτή η έρευνα. Ένα εντυπωσιακό και ενθαρρυντικό χαρακτηριστικό των μαθηματικών δομών όμως είναι ότι οι ιδιότητες συμμετρία και σταθερότητα που είναι υπεύθυνες για την απλότητα και την τάξη του σύμπαντός μας τείνουν να είναι γενικές, αποτελώντας περισσότερο τον κανόνα παρά την εξαίρεση.
Οι μαθηματικές δομές τείνουν να έχουν εκ φύσεως αυτές τις ιδιότητες και πρέπει να προστεθούν επιπρόσθετα αξιώματα για να τις βγάλουν από πάνω τους.
Η απλούστερη εξήγηση είναι συνήθως η καλύτερη
Επομένως, οι επιστημονικές θεωρίες των παράλληλων συμπάντων συνθέτουν μια ιεραρχία τεσσάρων επιπέδων, στην οποία τα σύμπαντα προοδευτικά γίνονται διαφορετικότερα από το δικό μας.
Μπορεί να έχουν διαφορετικές αρχικές συνθήκες (Επίπεδο I), διαφορετικές φυσικές σταθερές και σωματίδια (Επίπεδο II) ή διαφορετικούς φυσικούς νόμους (Επίπεδο IV). Το Επίπεδο ΙΙΙ είναι αυτό που έχει τραβήξει τα πάνδεινα τις τελευταίες δεκαετίες, επειδή είναι το μόνο που δεν προσθέτει ποιοτικά νέα είδη συμπάντων.
Την επόμενη δεκαετία, οι δραματικά βελτιωμένες κοσμολογικές μετρήσεις της μικροκυματικής ακτινοβολίας υποβάθρου και της κατανομής της ύλης του σύμπαντός μας σε μεγάλη κλίμακα, θα επιβεβαιώσουν ή θα αντικρούσουν τη φύση του Επιπέδου Ι, όταν θα έχουμε ακριβή αποτύπωση της καμπυλότητας και της τοπολογίας του χώρου.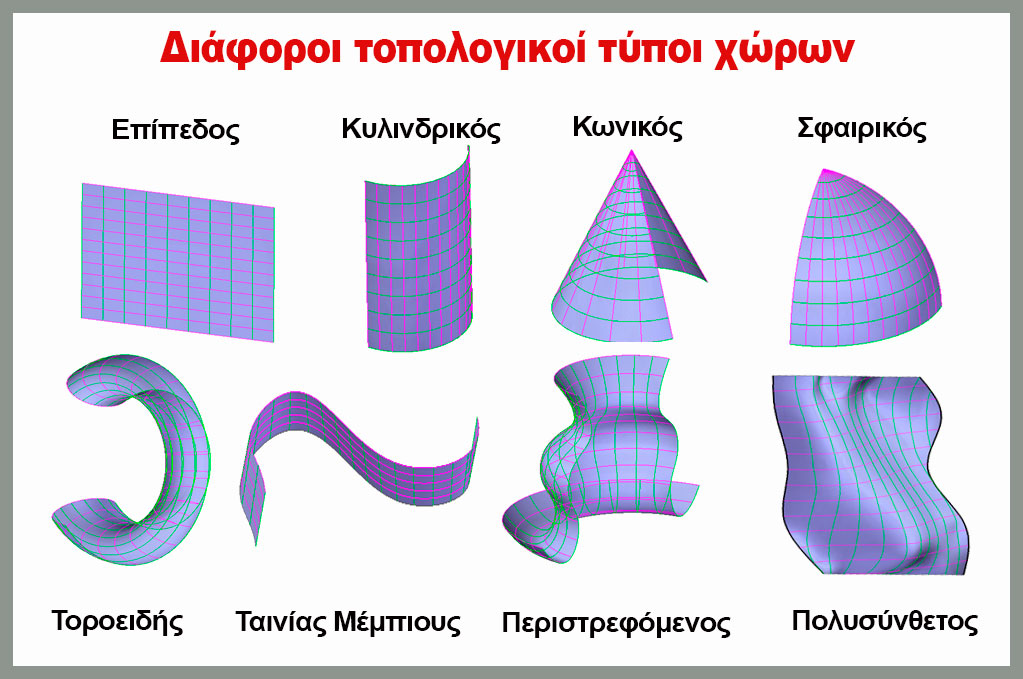

Διάφοροι τύποι τοπολογίας χώρου. Η επίσημη γεωμετρία μας είναι βασισμένη σε ένα επίπεδο, ευκλείδιο σύμπαν όπως το σχήμα επάνω αριστερά. Kάτω αριστερά, σύμπαν σε σχήμα τόρου (κουλουριού). Προσαρμογή – μετάφραση γραφήματος: “Απεροπία”
Αυτές οι μετρήσεις θα διερευνήσουν επίσης το Επίπεδο ΙΙ με τον πειραματικό έλεγχο της θεωρίας του χαοτικού αιώνιου πληθωρισμού. Η πρόοδος, τόσο στην αστροφυσική, όσο και στη φυσική υψηλών ενεργειών, θα πρέπει επίσης να διευκρινίσει την έκταση στην οποία οι φυσικές σταθερές εξαρτώνται από τις μεταβολές των παραμέτρων, αποδυναμώνοντας ή ενισχύοντας την περίπτωση του Επιπέδου ΙΙ.
Εάν πετύχουν οι προσπάθειες που καταβάλλονται για την κατασκευή κβαντικών υπολογιστών (σημ. μτφρ.: έχουν ήδη πετύχει), θα δώσουν περαιτέρω στοιχεία για το Επίπεδο ΙΙΙ, καθώς ουσιαστικά θα εκμεταλλευτούν τον παραλληλισμό του Πολυσύμπαντος επιπέδου ΙΙΙ για να εκτελούν παράλληλες υπολογιστικές πράξεις.
Τέλος, η επιτυχία ή η αποτυχία της μεγάλης πρόκλησης της σύγχρονης φυσικής —της ενοποίησης δηλαδή της Θεωρίας της Γενικής Σχετικότητας και της Κβαντικής θεωρίας Πεδίου— θα επηρεάσουν και τις απόψεις μας για το Επίπεδο IV (σημ. μτφρ.: ήδη βρισκόμαστε πολύ κοντά στην ενοποίηση).
Είτε θα βρούμε μια μαθηματική δομή που θα αντιστοιχεί ακριβώς στο σύμπαν μας, είτε θα χτυπήσουμε στον τοίχο των ακατανόητων συνεπειών των μαθηματικών και θα πρέπει να εγκαταλείψουμε το Επίπεδο IV.
Η γοητεία της παραδοξότητας
Πρέπει τελικά να πιστέψετε στα παράλληλα σύμπαντα ή όχι; Τα βασικά επιχειρήματα εναντίον τους είναι ότι είναι σπάταλα και παράξενα. Το πρώτο επιχείρημα είναι ότι οι θεωρίες που περιέχουν πολλαπλές υποθέσεις είναι ευάλωτες στην απλή λογική, επειδή υποδηλώνουν την ύπαρξη άλλων κόσμων που δεν μπορούμε ποτέ να παρατηρήσουμε.
Γιατί η φύση δεν κάνει οικονομία και πρέπει να είναι τόσο σπατάλη, επιδιδόμενη σε μια τέτοια πολυτέλεια όπως έναν άπειρο κόσμο που αποτελείται από διαφορετικούς κόσμους; Ωστόσο, αυτό το επιχείρημα μπορεί να στραφεί τελικά υπέρ ενός πολυσύμπαντος.
Τι ακριβώς θα σπαταλούσε η φύση; Σίγουρα όχι χώρο, μάζα ή άτομα. Το αδιαμφισβήτητο Πολυσύμπαν Επιπέδου Ι περιέχει ήδη ένα άπειρο ποσό κι από τα τρία, έτσι ποιος νοιάζεται αν η φύση σπαταλάει λίγο περισσότερα;
Το πραγματικό ζήτημα εδώ είναι η φαινομενική μείωση της απλότητας. Ένας σκεπτικιστής ανησυχεί για το που θα βρει όλες τις απαραίτητες πληροφορίες για να καθορίσει όλους αυτούς τους αθέατους κόσμους.
Αλλά ένα ολόκληρο σύνολο είναι συχνά πολύ απλούστερο από καθένα από τα μέλη του. Αυτή η αρχή μπορεί να γίνει πιο κατανοητή, αν χρησιμοποιήσουμε την έννοια του αλγοριθμικού περιεχομένου πληροφοριών. Σ’ έναν αριθμό, το αλγοριθμικό περιεχόμενο της πληροφορίας είναι με απλά λόγια το συντομότερο πρόγραμμα υπολογιστή που θα παράγει αυτόν τον αριθμό.
Για παράδειγμα, εξετάστε το σύνολο όλων των ακεραίων αριθμών. Ποιο είναι απλούστερο: το σύνολο ή μόνο ένας αριθμός; Αρχικά, ίσως να πιστεύετε ότι ένας απλός αριθμός είναι απλούστερος, αλλά ολόκληρο το σετ μπορεί να δημιουργηθεί από ένα αρκετά κοινό πρόγραμμα υπολογιστή, ενώ ένας μόνο αριθμός μπορεί να είναι πολύ μεγάλος. Επομένως, το σύνολο είναι πάντα απλούστερο.
Ομοίως, το σύνολο όλων των λύσεων στις εξισώσεις πεδίου του Αϊνστάιν είναι απλούστερο από μια επί μέρους λύση. Το πρώτο περιγράφεται με μερικές εξισώσεις, ενώ η τελευταία απαιτεί τεράστιες ποσότητες αρχικών δεδομένων μέσα σε κάποια υπερ-επιφάνεια.
Το συμπέρασμα είναι ότι η πολυπλοκότητα αυξάνεται όταν περιορίζουμε την προσοχή μας σε ένα συγκεκριμένο στοιχείο ενός συνόλου, παρά σ’ ολόκληρο το σύνολο, χάνοντας έτσι τη συμμετρία και την απλότητα που είναι εγγενείς στο σύνολο των στοιχείων.
Με αυτή την έννοια, τα πολυσύμπαντα υψηλότερου επιπέδου είναι απλούστερα. Η μετάβαση από το σύμπαν μας στο πολυσύμπαν Επιπέδου I εξαλείφει την ανάγκη καθορισμού των αρχικών συνθηκών. Πηγαίνοντας μετά στο επίπεδο ΙΙ η ανάγκη καθορισμού φυσικών σταθερών εξαλείφεται και το πολυσύμπαν επιπέδου IV εξαλείφει την ανάγκη να καθοριστεί οτιδήποτε.
Η αύξηση της πολυπλοκότητας προκύπτει από την υποκειμενική αντίληψη του παρατηρητή, μ’ άλλα λόγια από την οπτική του βατράχου. Σύμφωνα όμως με την οπτική του πουλιού, τα πολυσύμπαντα IV είναι πολύ απλά.
Τα παράπονα περί παραδοξότητας είναι αισθητικής φύσεως και όχι επιστημονικής, κι έχουν νόημα μόνο σύμφωνα με μια αριστοτέλεια κοσμοθεώρηση. Τι περιμέναμε δηλαδή; Να ρωτάμε μια σοβαρή ερώτηση σχετικά με τη φύση της πραγματικότητας, και να παίρνουμε μια απάντηση που να μην ακούγεται περίεργη;
Η εξέλιξη μας χάρισε διαίσθηση όσον αφορά την φυσική της καθημερινότητας που είχε αξία επιβίωσης για τους μακρινούς προγόνους μας, αλλά σήμερα κάθε φορά που ξεφεύγουμε από τον καθημερινό κόσμο, πρέπει να αναμένουμε ότι θα φαίνεται παράδοξος.
Ένα κοινό χαρακτηριστικό και των τεσσάρων επιπέδων πολυσυμπάντων είναι ότι η απλούστερη και αναμφισβήτητα η πιο κομψή θεωρία, περιλαμβάνει παράλληλα σύμπαντα εξ ορισμού.
Για να αρνηθούμε την ύπαρξη αυτών των συμπάντων, πρέπει να περιπλέξουμε τη θεωρία, προσθέτοντας πειραματικά μη υποστηριζόμενες διαδικασίες και αξιώματα ad hoc: πεπερασμένο χώρο, κατάρρευση κυματοσυνάρτησης και οντολογική ασυμμετρία.
Κατά συνέπειαν πρέπει να διαλέξουμε τι προτιμάμε τελικά ως πιο σπάταλο και πιο άκομψο: τα πολλά σύμπαντα ή τα πολλά λόγια; Ίσως τελικά συνηθίσουμε τις αλλόκοτες συμπεριφορές του κόσμου μας και αντιληφθούμε ότι η παραδοξότητά του είναι μέρος της γοητείας του.
– – – – – – – – – – – – – –
Δημοσιεύτηκε στο περιοδικό Scientific American τον Μάιο του 2003
ΠΗΓΕΣ:
Paralllel Universes, Max Tegmark, Scientific American
Evidence for Parallel Universes – Max Tegmark – YouTube
The True Science of Parallel Universes
http://www.rudyrucker.com
ΣΗΜΕΙΩΣΕΙΣ
[1] Μαξ Τέγκμαρκ: Αμερικανός φυσικός και κοσμολόγος σουηδικής καταγωγής. Έγραψε μια τετραδιάστατη έκδοση του παιχνιδιού υπολογιστή Tetris, ενώ ακόμη ήταν στο λύκειο. Σε ένα άλλο σύμπαν, επρόκειτο να γίνει ένας πολύ ακριβά αμειβόμενος προγραμματιστής. Στο σύμπαν μας, ωστόσο, έγινε καθηγητής φυσικής και αστρονομίας στο Πανεπιστήμιο της Πενσυλβανίας και εν συνεχεία στο Τεχνολογικό Ινστιτούτο της Μασαχουσέτης (ΜΙΤ). Ο Τέγκμαρκ είναι ειδικός στην ανάλυση της μικροκυματικής ακτινοβολίας υποβάθρου και της ομαδοποίησης των γαλαξιών. Μεγάλο μέρος της δουλειάς του είναι αφιερωμένο στην ανάλυση των παράλληλων συμπάντων, στην επεξεργασία πληροφοριών για την κβαντική αποσυνοχή και μελέτη της πιθανότητας ότι το πλάτος των διακυμάνσεων της μικροκυματικής ακτινοβολίας υποβάθρου, οι διαστάσεις του χωροχρόνου και οι θεμελιώδεις νόμοι της φυσικής μπορεί να διαφέρουν από τόπο σε τόπο.
Ο Τέγκμαρκ είναι ιδρυτής του Ινστιτούτου Θεμελιωδών Ερωτήσεων (Foundational Questions Institute) που ασχολείται με την έρευνα και τη διάχυση ερωτήσεων πάνω στις αρχές της φυσικής και της κοσμολογίας, συνιδρυτής του Ινστιτούτου του Μέλλοντος της Ζωής (που …αλληθωρίζει προς τον διανθρωπισμό), καθώς επίσης και συγγραφέας των βιβλίων «Το μαθηματικό σύμπαν μας» (Εκδ. Τραυλός, 2015) και Life 3.0: Being Human in the Age of Artificial Intelligence (Ζωή 3.0: O άνθρωπος στην εποχή της τεχνητής νοημοσύνης).
[2] Παρατηρήσιμο σύμπαν: Δεν πρέπει να συγχέουμε το παρατηρήσιμο σύμπαν με την πραγματική έκταση του σύμπαντός μας που εφόσον είναι σφαιρικό και πεπερασμένο, η διάμετρός του σήμερα είναι 93 δισεκατομμύρια έτη φωτός.
[3] Μικροκυματική ακτινοβολία υποβάθρου: ονομάζεται το ίχνος, ή υπόλειμμα της ακτινοβολίας που εξέπεμπε το σύμπαν όταν βρισκόταν σε κατάσταση εξαιρετικά μεγάλων θερμοκρασιών και πιέσεων. Αντιστοιχεί σε ακτινοβολία μέλανος σώματος, θερμοκρασίας 2,730 Κέλβιν και έρχεται από όλες τις κατευθύνσεις. Παρουσιάζει μεγάλη ισοτροπία και ομοιογένεια.
[4] Φράκταλ: μορφόκλασμα. Αναφέρεται σ’ ένα γεωμετρικό σχήμα που επαναλαμβάνεται αυτούσιο σε άπειρο βαθμό μεγέθυνσης, κάτι που ενισχύει τη θεωρία του ολογραφικού σύμπαντος. Σύμφωνα με τα λεγόμενα του διακεκριμένου φυσικού και προστατευόμενου του Αϊνστάιν, Ντέιβιντ Μπομ, το σύμπαν μας δεν είναι παρά δισδιάστατο ολόγραμμα, γι’ αυτό και κάθε επιμέρος τμήμα του περιέχει όλες τις πληροφορίες που περιέχονται στο συνολικό ολόγραμμα.
[5] Κλίμακα Κέλβιν: σύστημα μέτρησης της θερμοκρασίας στο Διεθνές Σύστημα Μονάδων. Το 0 Κέλβιν αντιστοιχεί στη χαμηλότερη δυνατή θερμοκρασία, ή απόλυτο μηδέν, δηλαδή στους -273,150 C
[6] Κουάρκ: στοιχειώδεις δομικοί λίθοι της ύλης. Συναντώνται κυρίως στο εσωτερικό πρωτονίων και νετρονίων, δηλαδή των σωματιδίων που απαρτίζουν τον πυρήνα κάθε ατόμου στο σύμπαν μας. Με βάση σύγχρονα πειραματικά δεδομένα, τα κουάρκ φαίνεται πως είναι κυριολεκτικά θεμελιώδη – δεν μπορούν δηλαδή να διαιρεθούν περαιτέρω.
[7] Κυματοσυνάρτηση: H κυματοσυνάρτηση που συνήθως συμβολίζεται με το ελληνικό γράμμα Ψ είναι η συνάρτηση που περιγράφει ένα κύμα. Σε αυτήν περιέχεται η πληροφορία για την κίνηση ενός σωματίου στο χώρο, αφού βάσει της θεωρίας του De Broglie (ντε Μπρολί) που επιβεβαιώθηκε και πειραματικά, ένα σωμάτιο συμπεριφέρεται σαν ένα κύμα. Όταν αυτό το μήκος κύματος είναι συγκρίσιμο με τις διαστάσεις του χώρου στον οποίο βρίσκεται, τότε εκδηλώνονται οι κυματικές ιδιότητες των σωματίων.
[8] Σρέτινγκερ: Διάσημος Αυστριακός φυσικός (1887-1961). Ασχολήθηκε κυρίως με την κβαντική φυσική, ανακαλύπτοντας την περίφημη κυματική εξίσωση που φέρει το όνομά του. Τιμήθηκε μαζί με τον Πολ Ντιράκ με το βραβείο Νόμπελ Φυσικής για τις εργασίες του πάνω στην ατομική θεωρία.
[9] Χώρος Χίλμπερτ: ονομάζεται ο χώρος των συναρτήσεων που χρησιμοποιείται στην κβαντομηχανική. Μαθηματικά ορίζεται ως ένας διανυσματικός χώρος και η έννοιά του είναι καθαρά μαθηματική. Επινοήθηκε από τον Γερμανό μαθηματικό Ντέιβιντ Χίλμπερτ (1862-1943). Το πιο απλό παράδειγμα χώρου είναι ο τρισδιάστατος ευκλείδειος χώρος (R3), ο οποίος χρησιμοποιείται ευρέως σε πολλά προβλήματα της φυσικής. Σε αντίθεση με τον χώρο R3, o χώρος Χίλμπερτ είναι απείρων διαστάσεων. H ουσιώδης διαφορά του χώρου Χίλμπερτ από τους απλούς διανυσματικούς χώρους έγκειται στο ότι αυτός κατοικείται από συναρτήσεις αντί για διανύσματα. Δηλαδή η βάση του χώρου και τα στοιχεία του αποτελούνται από συναρτήσεις.
[10] Νοητικό πείραμα του Σρέντινγκερ: Μια γάτα κλειδώνεται σε ένα ατσάλινο θάλαμο, μαζί με την εξής διάταξη (η οποία βρίσκεται με ασφάλεια εκτός εμβέλειας της γάτας): σε έναν μετρητή γκάιγκερ υπάρχει μια ελάχιστη ποσότητα ραδιενεργής ουσίας, τόσο μικρής, που κατά τη διάρκεια μιας ώρας ένα από τα άτομα διασπάται, αλλά επίσης ισοπίθανα, ίσως και όχι.

Απεικόνιση του νοητικού πειράματος της γάτας του Σρέτινγκερ
Αν συμβεί αυτό, ο μετρητής ενεργοποιείται και μέσω ενός διακόπτη (ρελέ) απελευθερώνει ένα σφυρί που σπάει μια μικρή φιάλη με υδροκυάνιο. Αν κάποιος αφήσει αυτό το σύστημα μόνο του για μια ώρα, μπορεί να υποθέσει ότι η γάτα είναι ακόμα ζωντανή, εάν στο μεταξύ δεν έχει διασπαστεί κάποιο άτομο. Η κυματοσυνάρτηση του συστήματος μπορεί να το εκφράσει, αν υπάρχει σε αυτή και η ζωντανή και η νεκρή γάτα αναμεμιγμένες ή διάχυτες εξίσου.
[11] Ρούντι Ράκερ: Αμερικανός μαθηματικός, επιστήμων υπολογιστών, συγγραφέας επιστημονικής φαντασίας και ζωγράφος, εμπνευστής του κινήματος κυβερνοπάνκ.
[12] Αναφέρεται στο λόγο της περιφέρειας προς τη διάμετρο ενός κύκλου, τη μαθηματική σταθερά π=3,14159265 Labels Περίεργα – Απίστευτα Loading… Νεότερη ανάρτηση Παλαιότερη Ανάρτηση
Article Source – ksipnistere.com